honestly while I agree that slightly longer keys wont be safe for long , but tbh I’m gonna sit a bit more on my 23-bit RSA keys before migrating

it produces its own oxygen , duh

oh gosh they are doing lobotomy again

btw 90% of all pedo porn is done by the feds in order to poison the well

i’d say 99% -> https://wikispooks.com/wiki/Pedophocracy […]

that’s certainly a take , the linked wiki page contains no relevant information

Agh I made a mistake in my code:

if (recalc || numbers[i] != (hashstate[i] & 0xffffffff)) {
	hashstate[i] = hasher.hash(((uint64_t)p << 32) | numbers[i]);
}

Since I decided to pack the hashes and previous number values into a single array and then forgot to actually properly format the values, the hash counts generated by my code were nonsense. Not sure why I did that honestly.

Also, my data analysis was trash, since even with the correct data, which as you noted is in a lineal correlation with n!, my reasoning suggests that its growing faster than it is.

Here is a plot of the incorrect ratios compared to the correct ones, which is the proper analysis and also clearly shows something is wrong.

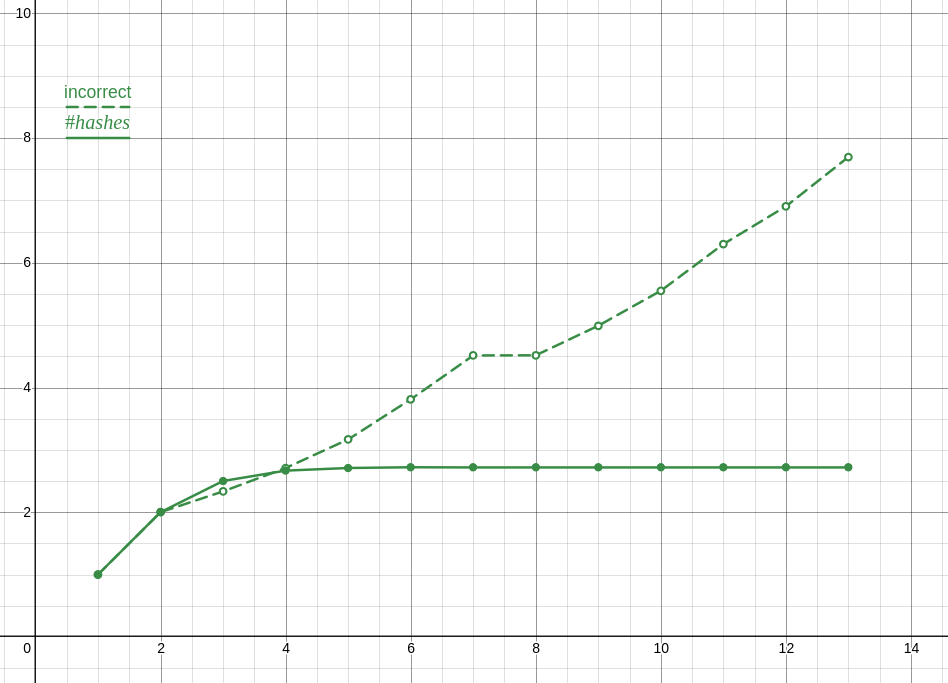
Anyway, and this is totally unrelated to me losing an internet argument and not coping well with that, I optimized my solution a lot and turns out its actually faster to only preform the check you are doing once or twice and narrow it down from there. The checks I’m doing are for the last two elements and the midpoint (though I tried moving that about with seemingly no effect ???) with the end check going to a branch without a loop. I’m not exactly sure why, despite the hour or two I spent profiling, though my guess is that it has something to do with caching?

Also FYI I compared performance with -O3 and after modifying your implementation to use sdbm and to actually use the previous hash instead of the previous value (plus misc changes, see patch).

you forgot about updating the hashes of items after items which were modified , so while it could be slightly faster than O((n!×n)²) , not by much as my data shows .

in other words , every time you update the first hash you also need to update all the hashes after it , etcetera

so the complexity is O(n×n + n×(n-1)×(n-1)+…+n!×1) , though I dont know how to simplify that

actually all of my effort was wasted since calculating the hamming distance between two lists of n hashes has a complexity of O(n) not O(1) agh

I realized this right after walking away from my devices from this to eat something :(

edit : you can calculate the hamming distance one element at a time just after rehashing that element so nevermind

honestly I was very suspicious that you could get away with only calling the hash function once per permutation , but I couldn’t think how to prove one way or another.

so I implemented it, first in python for prototyping then in c++ for longer runs… well only half of it, ie iterating over permutations and computing the hash, but not doing anything with it. unfortunately my implementation is O(n²) anyway, unsure if there is a way to optimize it, whatever. code

as of writing I have results for lists of n ∈ 1 … 13 (13 took 18 minutes, 12 took about 1 minute, cant be bothered to run it for longer) and the number of hashes does not follow n! as your reasoning suggests, but closer to n! ⋅ n.

link for the desmos page

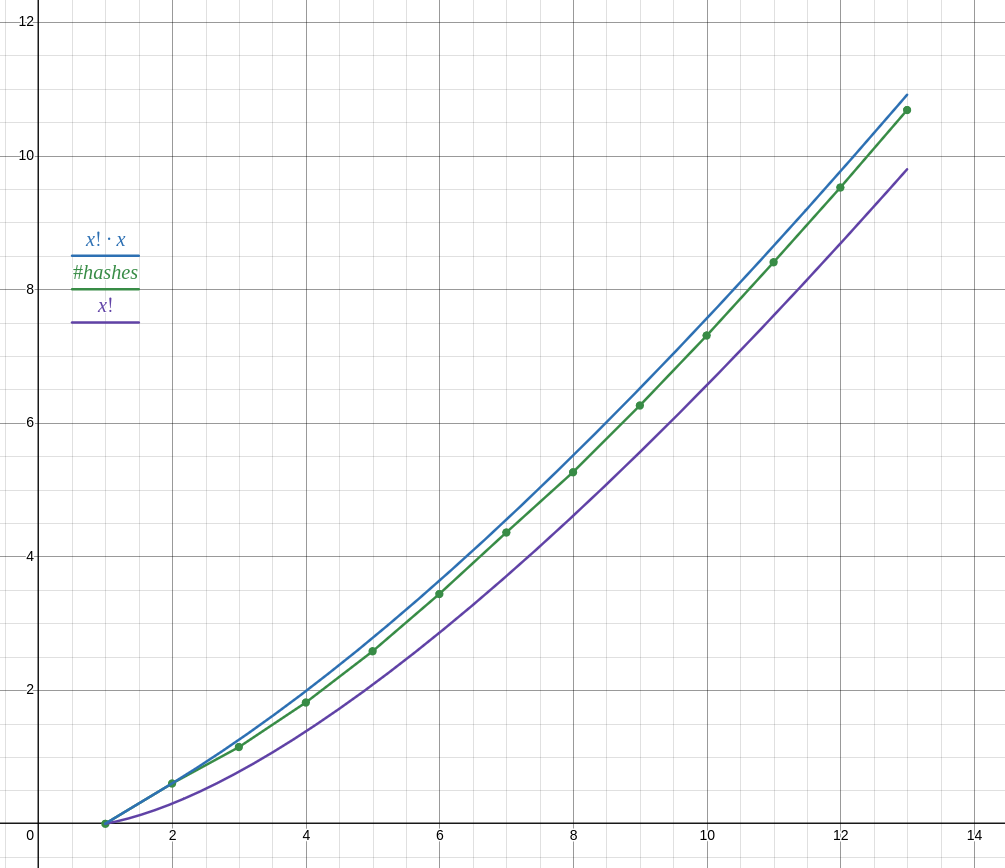
anyway with your proposed function it doesn’t seem to be possible to achieve O(n!²) complexity

also dont be so negative about your own creation. you could write an entire paper about this problem imho and have a problem with your name on it. though I would rather not have to title a paper “complexity of the magic lobster party problem” so yeah

unless the problem space includes all possible functions f , function f must itself have a complexity of at least n to use every number from both lists , else we can ignore some elements of either of the lists , therby lowering the complexity below O(n!²)

if the problem space does include all possible functions f , I feel like it will still be faster complexity wise to find what elements the function is dependant on than to assume it depends on every element , therefore either the problem cannot be solved in O(n!²) or it can be solved quicker

this would assume that finding the next prime is a linear operation , which is false

if I’m not mistaken , a example of a problem where O(n!²) is the optimal complexity is :

There are n traveling salespeople and n towns . find the path for each salesperson with each salesperson starting out in a unique town , such that the sum d₁ + 2 d₂ + … + n dₙ is minimised, where n is a positive natural number , dᵢ is the distance traveled by salesperson i and i is any natural number in the range 1 to n inclusive .

pre post edit, I realized you can implement a solution in 2(n!) :(

both Microsoft office and open/libre office files are zip files containing mostly XML so its not that bad actually , as long as you expose the files inside to git

sooooo you’re saying mountains are gay ?

I cannot read this as girls into crystals / girls into geology but my brain always interprets it as in girls who are (made of) crystal / girls who are (made of) geology

pretty sure that there are actually people who do believe the earth is flat

but yeah AFAIK the model that most flat earthers use does not allow for either lunar nor solar eclipses , requiring a fourth object to cause the effect

lmao the “high priority bug” is just a user error

honestly I use .hh/.cc which is quite nice IMO . you can also use .hpp/.cpp but I don’t like it personally

reminder that .H can be used as a c++ header extension , along with .C for source files

yeah but using mb/mB instead of M(i)b/M(i)B is a factor of 1 000 000 / 1 024 000 which is more than six magnitudes greater than 8

ah , for context I’m Lily