History

It is believed that the first definition of a conic section was given by Menaechmus (died 320 BC) as part of his solution of the Delian problem (Duplicating the cube). His work did not survive, not even the names he used for these curves, and is only known through secondary accounts. The definition used at that time differs from the one commonly used today. Cones were constructed by rotating a right triangle about one of its legs so the hypotenuse generates the surface of the cone (such a line is called a generatrix). Three types of cones were determined by their vertex angles (measured by twice the angle formed by the hypotenuse and the leg being rotated about in the right triangle). The conic section was then determined by intersecting one of these cones with a plane drawn perpendicular to a generatrix. The type of the conic is determined by the type of cone, that is, by the angle formed at the vertex of the cone: If the angle is acute then the conic is an ellipse; if the angle is right then the conic is a parabola; and if the angle is obtuse then the conic is a hyperbola (but only one branch of the curve).

Euclid (fl. 300 BC) is said to have written four books on conics but these were lost as well. Archimedes (died c. 212 BC) is known to have studied conics, having determined the area bounded by a parabola and a chord in Quadrature of the Parabola. His main interest was in terms of measuring areas and volumes of figures related to the conics and part of this work survives in his book on the solids of revolution of conics, On Conoids and Spheroids.

Diagram from Apollonius’ Conics, in a 9th-century Arabic translation

The greatest progress in the study of conics by the ancient Greeks is due to Apollonius of Perga (died c. 190 BC), whose eight-volume Conic Sections or Conics summarized and greatly extended existing knowledge. Apollonius’s study of the properties of these curves made it possible to show that any plane cutting a fixed double cone (two napped), regardless of its angle, will produce a conic according to the earlier definition, leading to the definition commonly used today. Circles, not constructible by the earlier method, are also obtainable in this way. This may account for why Apollonius considered circles a fourth type of conic section, a distinction that is no longer made. Apollonius used the names ‘ellipse’, ‘parabola’ and ‘hyperbola’ for these curves, borrowing the terminology from earlier Pythagorean work on areas.

Pappus of Alexandria (died c. 350 AD) is credited with expounding on the importance of the concept of a conic’s focus, and detailing the related concept of a directrix, including the case of the parabola (which is lacking in Apollonius’s known works).

Apollonius’s work was translated into Arabic, and much of his work only survives through the Arabic version. Islamic mathematicians found applications of the theory, most notably the Persian mathematician and poet Omar Khayyám, who found a geometrical method of solving cubic equations using conic sections.

A century before the more famous work of Khayyam, Abu al-Jud used conics to solve quartic and cubic equations, although his solution did not deal with all the cases.

An instrument for drawing conic sections was first described in 1000 AD by Al-Kuhi.

Table of conics, Cyclopaedia, 1728

Johannes Kepler extended the theory of conics through the “principle of continuity”, a precursor to the concept of limits. Kepler first used the term ‘foci’ in 1604.

Girard Desargues and Blaise Pascal developed a theory of conics using an early form of projective geometry and this helped to provide impetus for the study of this new field. In particular, Pascal discovered a theorem known as the hexagrammum mysticum from which many other properties of conics can be deduced.

René Descartes and Pierre Fermat both applied their newly discovered analytic geometry to the study of conics. This had the effect of reducing the geometrical problems of conics to problems in algebra. However, it was John Wallis in his 1655 treatise Tractatus de sectionibus conicis who first defined the conic sections as instances of equations of second degree. Written earlier, but published later, Jan de Witt’s Elementa Curvarum Linearum starts with Kepler’s kinematic construction of the conics and then develops the algebraic equations. This work, which uses Fermat’s methodology and Descartes’ notation has been described as the first textbook on the subject. De Witt invented the term ‘directrix’.

Application

Conic sections are important in astronomy: the orbits of two massive objects that interact according to Newton’s law of universal gravitation are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. See two-body problem.

The reflective properties of the conic sections are used in the design of searchlights, radio-telescopes and some optical telescopes. A searchlight uses a parabolic mirror as the reflector, with a bulb at the focus; and a similar construction is used for a parabolic microphone. The 4.2 meter Herschel optical telescope on La Palma, in the Canary islands, uses a primary parabolic mirror to reflect light towards a secondary hyperbolic mirror, which reflects it again to a focus behind the first mirror.

https://en.m.wikipedia.org/wiki/Conic_section

The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone. For a plane perpendicular to the axis of the cone, a circle is produced. For a plane that is not perpendicular to the axis and that intersects only a single nappe, the curve produced is either an ellipse or a parabola (Hilbert and Cohn-Vossen 1999, p. 8). The curve produced by a plane intersecting both nappes is a hyperbola (Hilbert and Cohn-Vossen 1999, pp. 8-9).

The ellipse and hyperbola are known as central conics.

Because of this simple geometric interpretation, the conic sections were studied by the Greeks long before their application to inverse square law orbits was known. Apollonius wrote the classic ancient work on the subject entitled On Conics. Kepler was the first to notice that planetary orbits were ellipses, and Newton was then able to derive the shape of orbits mathematically using calculus, under the assumption that gravitational force goes as the inverse square of distance. Depending on the energy of the orbiting body, orbit shapes that are any of the four types of conic sections are possible.

A conic section may more formally be defined as the locus of a point P that moves in the plane of a fixed point F called the focus and a fixed line d called the conic section directrix (with F not on d) such that the ratio of the distance of P from F to its distance from d is a constant e called the eccentricity. If e=0, the conic is a circle, if 0<e<1, the conic is an ellipse, if e=1, the conic is a parabola, and if e>1, it is a hyperbola.

https://mathworld.wolfram.com/ConicSection.html

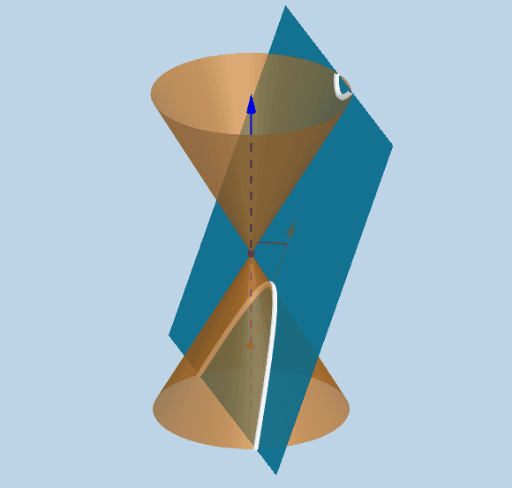
Conic sections are the result of intersecting the surfaces of a cone (normally, a double cone) and a plane. The three common conic sections are parabola, ellipse, and hyperbola.

How is a conic section obtained?

As we have mentioned in the previous section, these three conic sections are formed by finding the section intersected by a plane and a double cone.

The figures below show how the three conic sections are formed:

The images above show us how these conic sections or conics are formed when the plane intersects the cone’s vertex.

• If the cone’s plane intersects is parallel to the cone’s slant height, the section formed will be a parabola.
• We can see that the ellipse is the result of a tilted plane intersecting with the double cone. Circles are special types of ellipses and are formed when the cone is intersected by the horizontal plane.
• Hyperbolas are the result of the intersection between the vertical plane and the double cone.

These conics are called degenerate conics, and each of these is expected to contain a point, a line, and intersecting lines.

What are the common parts of the conic section?

Now that we know how to construct the three conic sections, we must learn the parts that they share in common.

Each conic section will look different from the other, but they still share common parts that can be used to identify them, such as their focus, directrix, and eccentricity.

• The focus of a conic refers to the point where the conic section is constructed and is defined.
• The directrix of a conic refers to the line that we use to construct a particular conic section.
• Given a point lying on the conic, the eccentricity reflects the ratio between the distance of the point and the focus and the distance of the point and the directrix.

Take a look at these three conics and notice how the directrix and foci (plural of focus) behave in a parabola, ellipse, and hyperbola.

We’ll learn more about each of this conic in the section below, but it helps to know how the focus and directrix would appear in each conic.

How to identify the conic section?

There are three ways to identify a conic section: using its graph’s shape, its eccentricity, or using the coefficients of the equation representing the conic section.

Remember these examples of conic sections as shown below to identify the conic sections, given their graphs easily.

Parabola

Ellipse

Hyperbola

How to identify conic sections from a general equation?

Let’s say we’re an equation of the form as shown below; there will be two ways for us to identify conic sections by inspecting the coefficients’ values.

𝐴⁢𝑥²+𝐵⁢𝑥⁢𝑦+𝐶⁢𝑦²+𝐷⁢𝑥+𝐸⁢𝑦+𝐹=0

Method 1: Rearrange the Equation

We can rearrange the given equation and see if it can be manipulated to be similar to the standard form of the three conic sections.

• Isolate all the terms on the right-hand side of the equation.
• Complete the perfect square whenever possible.
• After completing the square, make sure the remaining constants are on the left-hand side.
• Compare the new right-hand side equation with the conics’ standard forms and see if they can be categorized.

Method 2: Use the Coefficients of the Equations

• Using the coefficients, particularly , 𝐴⁢, 𝐵, and 𝐶, we can immediately identify the conics by finding the value of 𝐵²–4⁢𝐴⁢𝐶.
• If the result is negative and the conic exists, the conic is an ellipse (or a circle when 𝑎 =𝑏).
• If the result is equal to zero and the conic exists, the conic is a parabola.
• If the result is positive and the conic exists, the conic is a hyperbola.

Now that we know more important conic sections’ properties, we can also identify conic sections based on the equations that represent them.

https://www.storyofmathematics.com/conic-sections/